This site relies heavily on Javascript. You should enable it if you want the full experience. Learn more.

Curves

View
Edit

In mathematics a Curve is "a line that does not need to be straight". With that definition a large number of different curves exist each of which can be described by a mathematical formula.

Different mathematical curves

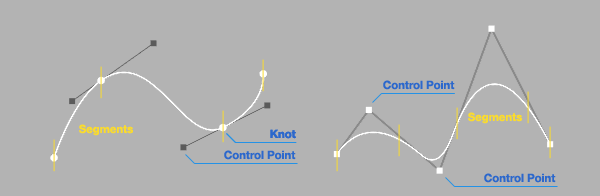
In computer graphics we're most interested in curves that can be described by mathematical formulas that are called polynomial functions. In order to be able to draw arbitrarily curved lines often multiple such curve-segments are combined to a Spline. The term "Spline" originates from an old draftsmen tool called a Flat Spline.

Curves that are piecewise defined by polynomial functions are called Splines

There are many different types of splines (hermite, bézier, catmull-rom, b-spline,..). but they all share the following key properties:

they are continuous at the Knots
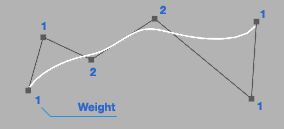
Control Points influence their shape

Splines with their segments, control points and knots

Bézier Spline

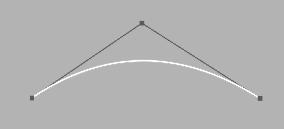Quadratic Bézier Curve with its Control Point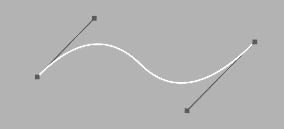

Cubic Bézier Curve with its two Control Points

The most popular Bézier curves are quadratic and cubic in nature as higher degree curves are expensive to draw, evaluate and not so intuitive to handle.

Characteristics

they cannot exactly describe circles and ellipses
they are a special cases of B-Spline

Related nodes

BezierEditor (2d)
BezierEditor (3d)
See also nodes from the 'BezierSegment' category.

BezierEditor nodes are operating with cubic Bézier splines.

See also:

Wikipedia on Bézier curves

B-Spline

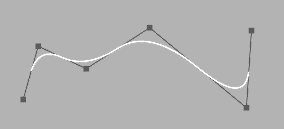An open B-Spline does not go through its control points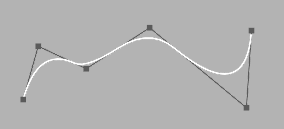

A clamped B-Spline which at least goes through its first and last control point

B-Spline is short for "basis spline".

Characteristics

they do not go through their control points
they have C2 continuity!
they are a special case of NURBS

in order to have a sharp corner in a B-Spline it takes three control-points at the same position
it is hard to insert a control point without changing the curve
it is hard to make a straight line
depending on its degree, changing one point changes large parts of the curve
they cannot exactly describe circles and ellipses.

In order to make it more intuitive to handle a B-Spline can also be constructed in a way it at least goes through its first and last control point.

See also:

Wikipedia on B-Splines

NURBS

A NURBS with its weighted control points

NURBS (short for "non uniform rational b-spline") are essentially B-Splines with a weight for each control point. If all its weights equal 1 the NURBS is a B-Spline.

NURBS generalizes both B-splines and Bézier curves
they can accurately represent circles and ellipses

Related nodes

NURBS (2d)
NURBS (3d)

See also:

Wikipedia on NURBS

Sources

Curves

Bézier Spline

Related nodes

B-Spline

Related nodes

NURBS

Related nodes

Shoutbox