Basic patch optimization using Expr

• Basic patch optimization using Expr
• Fist dummy test
• Let's add another operation
• Some trigonometry
• Conclusion

Expr (Value) is a node which allows you to evaluate a mathematical expression, represented as a string.

Fist dummy test

Let's do a test on a simple operation: x*2
As x*2 = x+x, i'm gonna try both ways using + (Value), * (Value), and expr with both operations.

On all patches I just run an = (Value) followed by AND (Boolean Spectral) to verify i have the same results for each operations.

I also put an lfo on the Phase pin of the spread, to make sure data changes all the time.

Here is the result in debug mode (Spread Count 50000):

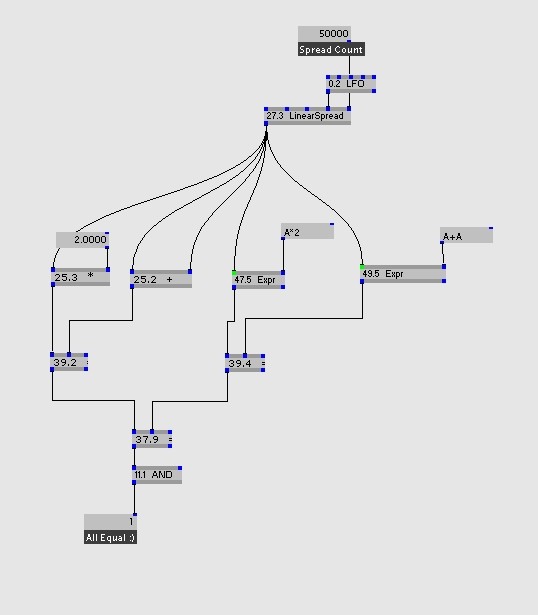
As we can see doing x+x or x*2 is fairly similar.

Expr performs a bit better on the A*2 part, but no big deal really.

In this simple operation case we can the see using the standard node outperforms Expr.

Let's add another operation

Now let's add something to our equation, and let's change it to x*2+1.

From now we need two nodes to perform this. We can still write the formula as a string.

I'm also gonna add up two other ways for Expr, having the 1 as a variable (so formula becomes x*2+y)

There goes the debug mode result.

As we can see, both + * technique stay roughly the same, so let's get interested by the expr part.

x*2+1 patched takes: 38.8+29.1 = 67.9
expr, with the 1 within the formula becomes 49.6
expr, with the 1 as parameter, becomes 71.2

So if our y will never change, we can see that using Expr outperforms patching.

Now if our y will change, using the nodes is still faster, but the gap in performance is closing very quickly.

So let's do a bit more complicated formula :)

Some trigonometry

Well ok, it's not that bas, we just gonna use (x*2+1)*sin(z)

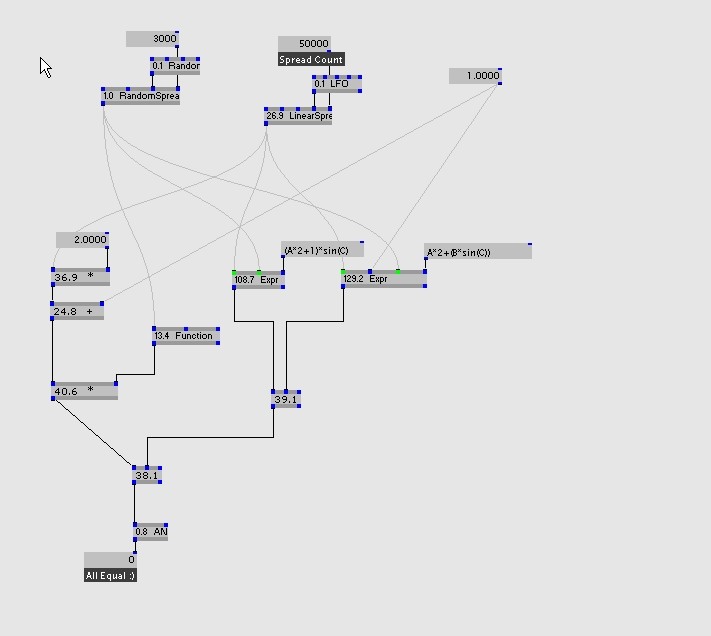
For the first try, we gonna use a spread count of 50000 for z, and 3000 for z.

Results as follow:

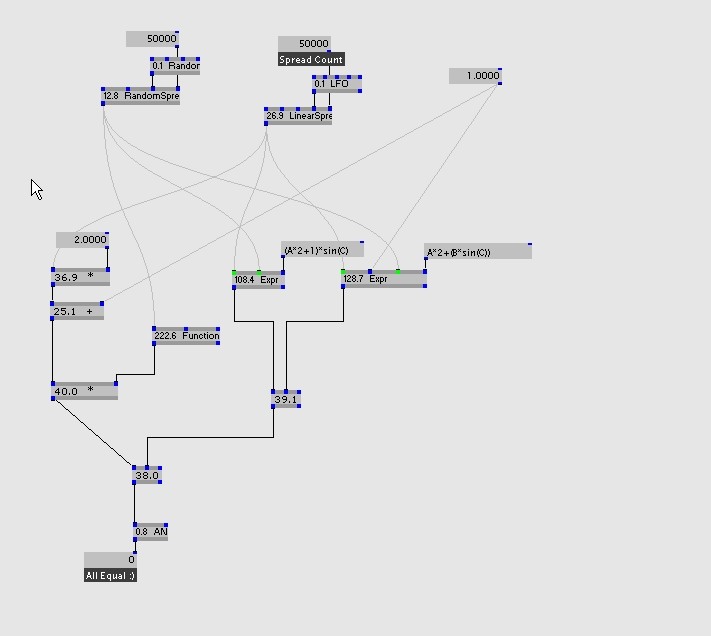
Now let's increase z spreadcount to 50000 as well:

What can we learn from that?

on a low spread count, our patch implementation does:
36.9+24.8+13.4+40.6=115.7

This is a bit faster than the Expr variable method, and a bit more than the Expr fixed method.

In this case please note that the sine function is evaluated only 3000 times then multiplied, whereas Expr evaluates it 50000 times at it fits in the expression.

On a high spread count for sine, the sine function on it's own takes 222.6, which is much more than the expr for the whole expression, so using expr makes your formula execute mush faster.

As an extra test on the 3000 spread count:
Function (Complex): 13.4
Expr (Value), using sin(A) : 5.1

Conclusion

• When a value doesn't change , it fits well in the Expr node as hardcoded in the formula.
• Trigonometric function is slow in comparison to Expr (would like to know why, possibly because of using complex numbers).
• If every variable has different spreadcount, some techniques are more interesting than others. Like if a variable has an expensive operation but a low spreadcount, it's much better to evaluate it separately and integrate the result in the equation.

by vux